Published on: Jul 01, 2022
Note: To better understand this blog, it is fundamental that you read our previous blogs “Reconfigurable Intelligent Surfaces” [1], “Have you ever heard (of) Beamforming?” [2].
As we have seen in previous blogs, the enhancement of wireless communications is being conceived with the help of various emerging technologies within 5G and beyond. One of these technologies is Reconfigurable Intelligent Surfaces (RISs), which is the topic of general interest of this blog. Here we present a scheme, developed by one of our ESRs, Juan Sanchez, to direct the reflection of electromagnetic waves, via a RIS, to a configurable direction [3]. The scheme aims to be optimal, as well as simple.
RISs can be regarded as passive – or quasi-passive – structures that manipulate impinging electromagnetic waves and can serve different purposes, such as “arbitrary reflection, complete absorption, focusing, collimation of waves, etc.”, as explained in [1]. Since they are passive structures, they can be regarded as part of the wireless environment, technically referred to as the wireless channel. Hence, the use of RISs ultimately gives the great possibility of partially controlling the properties of the wireless channel.

Fig. 1. Reconfigurable Intelligent Surface [4], together with a transmitting antenna at the bottom.
Let us focus on one of these purposes, namely the arbitrary reflection feature of RISs. A reflective RIS can direct incoming radiation from the impinging electromagnetic waves to a configurable direction, by using a technique known as beamforming, as also mentioned in [2]. Remember that beamforming can be realized by tuning the phase shift of the signal of interest at each element of an antenna array. This procedure also holds for RISs that have a discrete distribution of elements, known as Unit Cells (UCs). In Fig. 1, we can observe a commercial RIS with 256 UCs, arranged in a 16×16 rectangular array. The UCs are, in this case, analogous to antenna array elements. To apply beamforming, we need some information about the wireless channel, or reasonable assumptions about its properties.
Let us further focus on a simple scenario for communication from a base station (BS) to a user equipment (UE) – also referred to as downlink (DL) communication – where interference is significantly low and can be neglected. The BS takes the role of transmitter (TX), whereas the UE takes the role of the receiver (RX). Assuming that the most significant signal contribution comes from the wireless path from the TX to the RIS to the RX, the scenario can be depicted as in Fig. 2. We notice that a RIS can be composed of an arbitrary number of N elements – UCs, where N = N1*N2. The whole transmission area can be virtually “partitioned” into multiple independent sub-paths, given that there is no correlation among the different UCs.
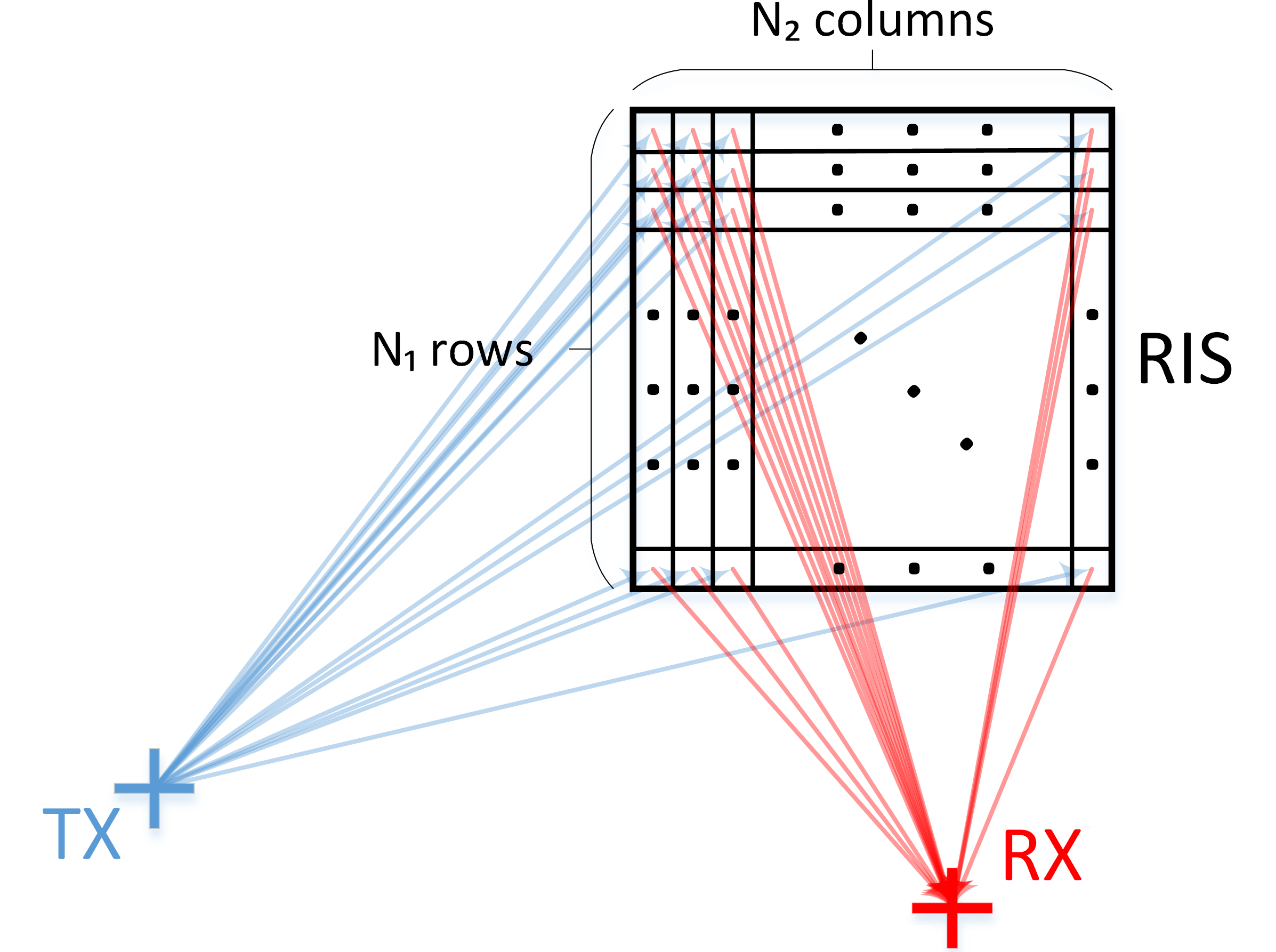
Fig. 2: Simplified geometric scenario for transmission through reflection at a RIS (Taken from [3]).
If we knew the relative position of the TX and the RX with respect to the RIS, and had the option to choose any phase shift we would like to apply to the signal impinging on the RIS, it would be straightforward to use this information to align the wavefronts by reverting the phase shift differences caused by the difference in distance at the propagation sub-paths. The subsequent received versions of the transmitted signal at the RIS can then be combined in such a way that they increase the received signal power at the RX. The beamforming scheme that does just that is referred to as Maximum Transmission Ratio (MRT) beamforming, and the combination of wavefronts is said to be coherent. However, RISs are not always capable of providing any possible phase shift; they rather provide a set of predefined – discrete – phase shifts which can be very limited in some cases. This causes misalignments in the wavefronts phases that impede a perfect combination of sub-paths and do not increase the received signal power to the maximum possible. Therefore, MRT beamforming is not optimal for discrete phase shift RISs.
We can improve this situation by tuning the phase shifts in such a way that the wavefronts have a better chance of combining coherently, even if the final received signal has a phase offset. That is, the received signal does not arrive in phase, but deviates. The resulting received power when tuning with a limited set of phase shifts will not be as high as the received power when tuning with an infinite set of phase shifts at the RIS. However, the procedure will reach the optimality allowed by the predefined set of phase shifts. Additionally, correction of the resulting deviation can be then easily achieved by applying other techniques. Furthermore, the complexity of finding the optimal phase shift combination is directly proportional to the number of UCs. In contrast, testing out all possible phase shift combinations allowed by the RIS would require a combinatorial complexity proportional to a power of the number of UCs. This ultimately means, we achieve optimal beamforming gains at low complexity by using the modified MRT beamforming scheme suggested [3].
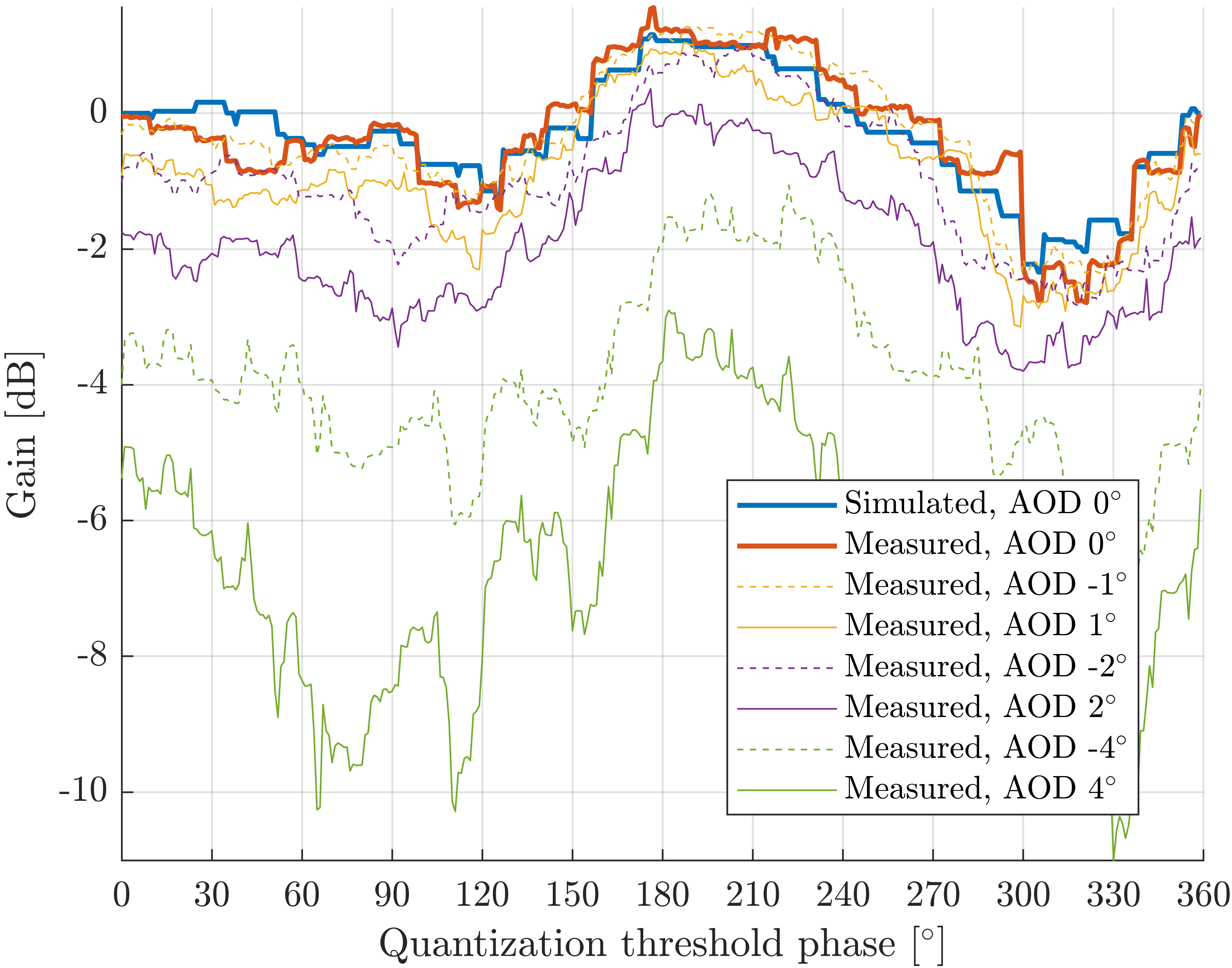
Fig. 3. Simulated and measured RIS gains vs. quantization threshold phase, with and without deviations of Angle of Departure (AOD) from the RIS to the RX (Taken from [3]).
To confirm the theory developed so far, measurements for the previously explained scenario were carried out in the mmWave frequency range, namely 28GHz. On top of that, angular deviations representing inaccuracies of the RX position were introduced into the input parameters of the beamforming scheme. The results from Fig. 3 show the relative gain – in decibels – of the beamforming scheme depending on the resulting signal’s phase offset that the phase shifts at the UCs targeted. The targeted phase offset is referred to as the quantization threshold phase here, and is measured in angle units – degrees in this case. The curves from Fig. 3 allow us to draw multiple conclusions. First, the simulation of the beamforming theory agrees with the actual measurements. It is clear that greater deviations between the estimated position and the actual position of the RX translate into overall losses, since the beamforming scheme of the RIS does not reflect the incoming radiation to the direction of the RX. Second, the dependency of the RIS gain on the quantization threshold phase still holds after deviations in the RX position. This shows that the proposed beamforming scheme is robust against them. Third, deviations in the RX position increase the influence of the choice of quantization threshold phase on the RIS gain. For perfect knowledge of the position of the RX, choosing the right quantization threshold phase can imply gains of up to 4 decibels. For deviations of 4 degrees in the RX angle to direct the radiation, choosing the right quantization threshold phase can imply gains of up to 8 decibels.
If you want to understand the concept in more technical depth, and look at exciting results from actual mmWave measurements, you can read the article “Optimal, Low-Complexity Beamforming for Discrete Phase Reconfigurable Intelligent Surfaces” [3].
If you were able to stick until the end and can’t wait for more content and want to know about us and our projects, you can always follow our social media channels.
Citations
[1] MINTS. Blog: Have you ever heard (of) Beamforming? Available online at: https://b5g-mints.eu/blog9/
[2] MINTS. Blog: Reconfigurable Intelligent Surfaces. Available online at: https://b5g-mints.eu/ris-blog6/
[3] J. Sanchez, E. Bengtsson, F. Rusek, J. Flordelis, K. Zhao and F. Tufvesson, “Optimal, Low-Complexity Beamforming for Discrete Phase Reconfigurable Intelligent Surfaces,” 2021 IEEE Global Communications Conference (GLOBECOM), 2021, pp. 01-06, doi: 10.1109/GLOBECOM46510.2021.9685226.
[4] L. Yezhen, R. Yongli, Y. Fan, X. Shenheng, and Z. Jiannian, “A novel 28 GHz phased array antenna for 5G mobile communications,” ZTE Communications, vol. 18, no. 3, pp. 20–25, 2020.





